Los humanos, un Macguffin matemático

Siempre que escucho la palabra “Macguffin” mi mente se va hacia el gran cineasta británico Alfred Hitchcock (1899-1980), autor de grandes películas como La ventana indiscreta (1954), Vértigo (1958), Con la muerte en los talones (1959), Psicosis (1960) o Los pájaros (1963). Y más concretamente me remite al libro El cine según Hitchcock, que recoge la entrevista que le hizo el cineasta francés Francois Truffaut (1932-1984), un libro de cuya lectura he disfrutado en varias ocasiones.

¿Qué es el Macguffin?

El Macguffin, término acuñado por el maestro del suspense Alfred Hitchcock, es un objeto, persona, situación o suceso necesario para impulsar la trama y la motivación de los personajes, pero insignificante, sin importancia o irrelevante en sí mismo. Como diría Truffaut “es el pretexto”.

Por ejemplo, en las películas de espías suele ser un secreto o unos documentos, que hacen que la trama se desarrolle, pero que realmente da igual cuál sea el secreto o el contenido de los documentos. Como afirmó el propio Hitchcock, “el Macguffin es lo que persiguen los espías, pero al público le da igual”. En la película Con la muerte en los talones, el protagonista, encarnado por el actor estadounidense Cary Grant (1904-1986), es un agente publicitario que es confundido con un agente del gobierno por unos espías e intentan asesinarlo, motivando la huida del publicista para salvar su vida. Mientras que en la película Psicosis el Macguffin es el robo de un dinero y la posterior huida de su protagonista femenina, interpretada por la actriz estadounidense Vera Miles (1929), que provoca que se esconda en un pequeño hotel regentado por el tímido Norman Bates, que interpretaba el actor estadounidense Anthony Perkins (1932-1992), y que era realmente la parte central de la película. Otro ejemplo interesante es la estatuilla de la película El halcón maltés (1941), interpretada por Humphrey Bogart, Mary Astor y Peter Lorre, y basada en la novela negra homónima del escritor estadounidense Dashiell Hammett (1894-1961), que es el objeto de deseo de una serie de personajes de dudosa moral.

Para finalizar con los ejemplos, un Macguffin esclarecedor, más moderno y en otro tipo de película, como es The Blues Brothers (1980), donde los personajes encarnados por los actores estadounidenses John Belushi (1949-1982) y Dan Aykroyd (1952), intentan conseguir el dinero necesario para salvar el orfanato en el cual se criaron, lo cual no es más que la excusa para realizar un viaje con el objetivo de reunir a los miembros de un grupo musical y llenar ese viaje de humor y música, buena música de blues y soul.

En el libro El cine según Hitchcock, el maestro del suspense explicaba el origen del término de la siguiente forma.

Y ahora, conviene preguntarse de dónde viene el “MacGuffin”. Evoca un nombre escocés y es posible imaginarse una conversación entre dos hombres que viajan en un tren. Uno le dice al otro: “¿Qué es ese paquete que ha colocado en la red?” Y el otro contesta: “Oh, es un Mac Guffin”. Entonces el primero vuelve a preguntar: “¿Qué es un Mac Guffin?” Y el otro: “Pues un aparato para atrapar a los leones en las montañas Adirondaks”. El primero exclama entonces: “¡Pero si no hay leones en las Adirondaks!” A lo que contesta el segundo: “En ese caso no es un Mac Guffin”.

Esta anécdota demuestra el vacío del Mac Guffin … la nada del Mac Guffin.

Los humanos, de Matt Haig

La novela a la que vamos a dedicar esta entrada del Cuaderno de Cultura Científica, Los humanos (2013), del escritor británico Matt Haig (1975), contiene un Macguffin matemático. Pero vayamos por partes. Primero presentemos brevemente a su autor.

Matt Haig es un periodista y escritor inglés, que escribe tanto para adultos, como para jóvenes. Estudió Inglés e Historia en la Universidad de Hull. Entre sus libros nos encontramos novelas como Los humanos (2013), Cómo detener el tiempo (2017), La biblioteca de la medianoche (2020) o La vida imposible (2024), cuya protagonista es matemática; libros para jóvenes como Shadow Forest: el bosque de las sombras (2007), El chico que salvó la navidad (2015), La duendecilla sincera (2018) o Evie, la amiga de los animales (2019), y libros de no ficción como Razones para seguir viviendo (2015), Apuntes sobre un planeta estresado (2018) o El libro de la esperanza (2021).

Respecto a la novela Los humanos, lo primero es recomendar a las personas que estáis leyendo esta entrada que la leáis, no porque sea una novela relacionada con las matemáticas, sino porque es una novela interesante y muy divertida.

Pero para hablar de esta novela podemos empezar por la sinopsis escrita por la editorial:

El profesor Andrew Martin de la Universidad de Cambridge acaba de descubrir el secreto de los números primos, encontrando al mismo tiempo la clave que garantizará el fin de la enfermedad y la muerte. Convencidos de que los secretos de los números primos no pueden dejarse en manos de una especie tan primitiva como los humanos, los vonadorianos, una civilización extraterrestre mucho más evolucionada, envían a un emisario para hacer desaparecer a Martin y a su descubrimiento. Y así es como un vonadoriano con el aspecto externo de Martin aparece con la misión de matar a la esposa, al hijo y al mejor amigo del profesor, pero no puede dejar de sentirse fascinado por esa fea especie y sus costumbres incomprensibles.

El punto de partida de la novela es que el matemático y profesor de la Universidad de Cambridge (Gran Bretaña) Andrew Martin ha demostrado la llamada hipótesis de Riemann, uno de los problemas matemáticos abiertos, es decir, que está aún por resolverse, más importantes. De hecho, la hipótesis de Riemann es uno de los siete “problemas del milenio” que anunció el Instituto Clay de Matemáticas en el año 2000, con una recompensa de un millón de dólares para quien lo resolviese. Más aún, este problema ya estaba en la lista de los 23 problemas que recogió el matemático alemán David Hilbert (1862-1943) en el Congreso Internacional de Matemáticos de 1900, como problemas más importantes para el nuevo siglo xx.

Sin embargo, para una civilización extraterrestre, los vonadorianos, este es un conocimiento demasiado poderoso, que en manos de los humanos podría poner en peligro el equilibrio del universo y provocar su destrucción. Por este motivo, deciden reemplazar a Martin por un clon alienígena, que es realmente el protagonista de esta historia narrada por él mismo, y borrar toda evidencia de su descubrimiento, destruyendo los documentos relacionados con la demostración, los rastros digitales de la misma o las personas que hayan podido tener algún conocimiento de esta prueba, como la familia del matemático, su mujer y su hijo, y alguno de sus colegas.

Resulté ser un hombre casado de 43 años, la mitad exacta de una vida humana. Tenía un hijo. Era el profesor que acababa de resolver el enigma matemático más importante al que se habían enfrentado los humanos. Apenas tres horas antes había hecho progresar la especie humana más allá de lo que cualquiera habría podido imaginar.

La hipótesis de Riemann no es más que un pretexto, es decir, el Macguffin de esta historia, para contarnos de forma divertida cómo nos vería un extraterrestre a los terrícolas y hablar de lo que significa ser humano, del amor, la amistad, la familia, las relaciones humanas, los conflictos, la vida o la muerte.

Las matemáticas de los vonadorianos

Antes de entrar en materia, un pequeño comentario sobre el hecho de que los vonadorianos son una civilización extraterrestre para la cual las matemáticas son extremadamente importantes y un conocimiento esencial para ellos. Para que nos hagamos una idea de esto, incluyo algunas sencillas citas de la novela, que son pensamientos del vonadoriano protagonista.

La primera:

Yo nunca quise que me mandasen aquí. Se trataba de una tarea que, tarde o temprano, alguien tenía que asumir y, después de la charla que di en el Museo de las Ecuaciones Cuadráticas –que muchos tacharon de blasfemia, de supuesto crimen contra la pureza matemática–, a los anfitriones [los dirigentes de los vonadorianos] les pareció el castigo perfecto.

La segunda:

Por supuesto, en teoría aquella era mi ciudad […]. La falta de imaginación geométrica me tenía fascinado: no había ni tan siquiera un decágono a la vista. […] Pronto aprendería que en las ciudades todo es una tienda. Son a los moradores de la Tierra lo que las cabinas de ecuaciones son a los vonadorianos.

La tercera:

Allá de donde venimos la tecnología que hemos creado sobre las bases de nuestro entendimiento supremo y exhaustivo de las matemáticas nos ha supuesto no solo la posibilidad de atravesar grandes distancias, sino también de reajustar nuestros propios componentes biológicos, renovarlos y reponerlos. Estamos equipados psicológicamente para tales progresos. Nunca hemos vivido una guerra civil. Nunca anteponemos los deseos individuales a las necesidades del colectivo.

En general, las citas matemáticas de la novela tienen un objetivo literario y no rigurosidad matemática. Por ejemplo, en cierto momento el vonadoriano clon de Andrew Martin se queja de que el orden de prioridad de las noticias en televisión es incomprensible para él y se sorprende de que no hable de “nuevas observaciones matemáticas” (lo cual es un comentario bastante indefinido y confuso) o de “polígonos todavía por descubrir” (también bastante impreciso e incluso que puede considerarse equívoco).

La hipótesis de Riemann

A pesar de que la hipótesis de Riemann es solamente una excusa para hablar de los humanos, de la humanidad, Matt Haig sí intenta explicar en la novela, de forma muy sencilla y bastante literaria, en qué consiste la misma o, al menos, algunas ideas relacionadas con ella.

Así, cuando el vonadoriano con aspecto de Andrew Martin descubre en el ordenador del matemático de la Universidad de Cambridge el documento que contiene la demostración de la hipótesis de Riemann, hay un pequeño capítulo de la novela dedicado a los números primos y su distribución dentro de los números naturales (por cierto que una introducción a estos temas puede leerse en las entradas del Cuaderno de Cultura Científica Buscando lagunas de números no primos y El poema de los números primos, así como en el libro La gran familia de los números, que se menciona en la bibliografía), que comentaremos a continuación, aprovechando el texto de la novela.

Pero antes, así es como describe Matt Haig al autor de la hipótesis, el matemático alemán Bernhard Riemann (1826-1866).

Aprendí algo más sobre Bernhard Riemann, un niño prodigio alemán horrorosamente tímido que vivió en el siglo xix y que, ya desde una edad temprana, demostró su habilidad excepcional con los números, antes de sucumbir a su carrera de matemático y a la serie de crisis nerviosas que minaron su adultez. Más tarde descubriría que ese era uno de los problemas fundamentales que tienen los humanos con la comprensión numérica: simple y llanamente, su sistema nervioso no está capacitado.

La verdad es que no dice gran cosa, salvo que era un niño prodigio y que “sufría crisis nerviosas”, sobre una de las grandes mentes matemáticas de la historia, que realizó avances revolucionarios en todas las áreas de las matemáticas en las que trabajó, en particular, el análisis matemático, la geometría diferencial y la teoría de números. Muchos son los conceptos y resultados matemáticos asociados a su nombre, como la integral de Riemann, las ecuaciones de Cauchy-Riemann, las superficies de Riemann, la geometría riemanniana, el tensor de curvatura de Riemann, la función zeta de Riemann o la hipótesis de Riemann, entre otras.

Los números primos

Pero vayamos con los números primos. El primer párrafo sobre los mismos, que nos narra el vonadoriano, es el siguiente.

Los números primos vuelven a la gente loca, pero literalmente, sobre todo por la cantidad de enigmas que quedan sin resolver. Lo único que parecían saber es que un primo es un número entero que solo puede dividirse por 1 y por sí mismo, pero, más allá de eso, se dan de bruces con un problema tras otro.

La verdad es que es un comentario bastante simplista, puesto que viene a decir que el único conocimiento que se tiene sobre los números primos es su definición, es decir, que son aquellos números naturales que solamente se pueden dividir por 1 y por ellos mismos. Por ejemplo, el número 25 no es primo ya que se puede dividir por 5, mientras que el número 19 sí es primo, ya que solamente es divisible por el 1 y él mismo, al igual que lo son los números 2, 3, 5, 7, 11 y 13, entre otros. Sin embargo, los humanos llevamos más de dos milenios investigando sobre los números primos y obteniendo muchos e importantes resultados, como que existen infinitos números primos, como ya demostraron los antiguos griegos, que todo número natural se puede expresar de forma única como producto de números primos (el teorema fundamental de la aritmética), que la función contador de números primos, es decir, para cada número x, la cantidad de números primos menores o iguales que x se aproxima por la función x/Ln x (el teorema de los números primos), y así existen miles y miles de resultados más que podríamos añadir. Cabe mencionar que existen muchos libros dedicados solo a los resultados sobre los números primos, de los que mencionaremos aquí cuatro en clave más divulgativa, por si hay alguien interesado: 1) Prime Numbers, The Most Mysterious Figures in Math (David Wells, John Wiley & Sons, 2005); 2) The Little Book of Bigger Primes (Paulo Ribenboim, Springer Verlag, 2004); 3) La música de los números primos (Marcus du Sautoy, Acantilado, 2007); 4) Los números primos, un largo camino al infinito (Enrique Gracián, RBA, 2010).

Aunque después del párrafo anterior, sí menciona alguno de los conocimientos que la humanidad ha alcanzado sobre los números primos, casi siempre expresado de una forma más literaria, o incluso poética, que matemática. Por ejemplo, afirma que se conoce que hay infinitos números primos (la sencilla y hermosa demostración de los griegos podéis leerla en la entrada Buscando lagunas de números no primos), pero además menciona que son numerables, es decir, que se pueden contar (sobre los conjuntos infinitos podéis leer la serie de entradas titulada El infinito en un segmento: uno, dos y tres), de la siguiente forma.

Saben que el total de todos los números primos es igual al total de todos los números, pues ambos sumarían infinitos. Para el humano medio, esto constituye un hecho bastante desconcertante, pues ciertamente tienen que existir más números aparte de los primos. Tan imposible les resulta asimilar que, al enfrentarse al tema, más de uno se ha metido un revólver en la boca, ha apretado el gatillo y se ha volado los sexos.

Aquí realmente está mezclando dos temas apasionantes e importantes, primero que hay infinitos números primos, que puede entenderse bien por sí solo, pero a la vez nos habla de que hay tantos como números naturales, hecho que está relacionado con la dificultad de entender el infinito y sus paradojas, como lo mencionado, que una parte del conjunto (los números primos) tenga tantos elementos como todo el conjunto (los números naturales). Aunque este segundo tema es un poco complejo para las personas que lean la novela, es muy exagerado decir que “tan imposible les resulta asimilar que, al enfrentarse al tema, más de uno se ha metido un revólver en la boca, ha apretado el gatillo y se ha volado los sexos”, aunque tenemos que entender que esto es literatura y no divulgación de las matemáticas.

El siguiente párrafo dice lo siguiente:

Los humanos también han llegado a entender que los números primos se parecen mucho al aire terráqueo. Cuánto más arriba subes, menos hay. Por ejemplo, hay 25 números primos menores que 100, pero solo 21 entre 100 y el 200 y solo 16 entre 1.000 y 1.100. Sin embargo, a diferencia de aire en la Tierra, no importa lo mucho que subas en la escala de los números, siempre habrá algún número primo. Por ejemplo, 2.097.593 es primo y hay millones más entre ese y, pongamos, 4314398832739895727932419750374600193. En consecuencia, podemos decir que la atmósfera de los números primos recubre todo el universo.

La primera parte ofrece el primer comentario sobre la distribución de los números primos dentro de los naturales, que es el tema central sobre el que versa la hipótesis de Riemann. Y efectivamente es así. Como se comentaba en la entrada Buscando lagunas de números no primos, entre los 100 primeros números hay 25 primos, es decir, 1 de cada 4 números es primo. Sin embargo, si miramos entre los 1.000 primeros números, resulta que hay 168 que son primos, 1 de cada 6 números. Un porcentaje menor. Y así, como podemos ver en la siguiente tabla, según vamos ampliando la cantidad de números considerados, existe un menor porcentaje de números primos. Luego según vamos avanzando en la recta de números naturales, los números primos van siendo cada vez más infrecuentes, y los números compuestos van ocupando más el espacio dentro de los números naturales.

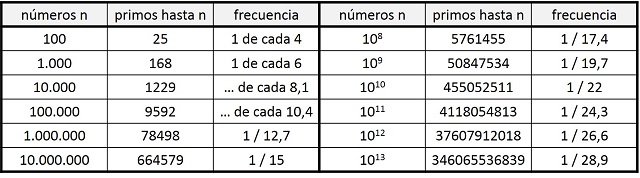
Sin embargo, el segundo comentario solo es una forma diferente y poética de volver a afirmar que existen infinitos números primos.

La distribución de los números primos

El texto del capítulo “Números primos” sigue asi:

En 1859, no obstante, en la Academia de Berlín, un Bernhard Riemann cada vez más enfermo enunció la que sería la hipótesis más estudiada y celebrada de todas las matemáticas. Afirmaba que había un patrón, o al menos lo había para los primeros mil números primos. Y era bello, cristalino e involucraba algo llamado “función zeta”, una especie de máquina mental, una curva de aspecto complejo que servía para investigar las propiedades de los primos. Si los colocabas en ella, formaban un orden en el que nadie se había fijado con anterioridad: ¡un patrón! ¡La distribución de los números primos no era arbitraria!

Una vez más mencionemos que esto no es un texto de divulgación de las matemáticas, sino literatura, ya que lo afirmado en el anterior párrafo hay que cogerlo con pinzas, pero como lector tengo que entender la intención narrativa del autor de la novela.

Para empezar, podemos considerar que la hipótesis de Riemann es una de las conjeturas más importantes y estudiadas, no en vano estaba entre los 23 problemas de Hilbert (en 1900) y entre los siete problemas del milenio (en 2000), pero hay otros problemas matemáticos también importantes y muy estudiados, como el último teorema de Fermat, conjeturado por el matemático francés Pierre de Fermat (1601-1665) hacia 1637 y demostrado por el matemático británico Andrew Wiles en 1995 (puede leerse sobre esta cuestión en la entrada Euler y el último teorema de Fermat); la conjetura de Poicaré, formulada por el matemático francés Henri Poincaré (1854-1912) en 1904 y demostrada por el matemático ruso Gregori Perelman en 2006 (véase la entrada La conjetura de Poincaré-Perelman-Miander); o el problema del quinto postulado de Euclides y la existencia de las geometrías no euclídeas, un problema que tardó más de dos milenios en resolverse, por matemáticos como Nikolai Lobachevski (1752-1856) y János Bolyai (1802-1860); o incluso problemas matemáticos que permanecen abiertos, como la conjetura de Goldbach, formulada por el matemático prusiano Christian Goldbach (1690-1764) en 1742 (véase la entrada La conjetura de Goldbach); o cualquiera de los problemas del milenio, que son la conjetura de Birch y Swinnerton-Dyer, en teoría de números algebraica; la conjetura de Hodge, en geometría algebraica; la solución de las ecuaciones de Navier-Stokes de la mecánica de fluidos; el problema P = NP, en ciencias de la computación; la conjetura de Poncaré, en topología (ya resuelta en 2006); el problema de la masa en la teoría de Yang-Mills, en la teoría cuántica de campos; y la mencionada hipótesis de Riemann, en análisis complejo y teoría de números primos, que es una de las más importantes y conocida.

Lo siguiente que vamos a comentar es la frase “afirmaba que había un patrón, o al menos lo había para los primeros mil números primos”, a la que podemos ponerle algunos peros matemáticamente hablando. Decir que había un patrón es ambiguo y simplista, aunque a Matt Haig le pueda valer para la novela.

Desde la matemática griega se ha intentado descubrir, sin éxito, la existencia de algún patrón en la distribución de los números primos dentro de los naturales, pero, como decía el matemático suizo Leonhard Euler (1707-1783), este será uno de esos misterios que la humanidad nunca será capaz de desvelar.

No existe ninguna fórmula que nos permita determinar cuál es el número primo n-ésimo, para cualquiera que sea la posición n, ni una expresión matemática que posibilite, conocidos todos los primos hasta uno dado, obtener el siguiente.

Aunque, una aproximación a la distribución de los números primos es el estudio de la función contador de números primos. Dado un número x se define pi(x) como la cantidad de primos menores, o iguales, que x. Si se observan los números primos hasta 100 se puede comprobar que pi(20) = 8 (que son 2, 3, 5, 7, 11, 13, 17 y 19) o pi(100) = 25 (que son, además de los anteriores, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73 79, 83 89 y 97). En la siguiente tabla se muestra el valor de la función contador de números primos (x) para las primeras potencias de 10, junto con la densidad (x) / x –la proporción de números primos respeto a los naturales, hasta x– y la frecuencia, x / (x) –cuántos números naturales hay por cada primo, hasta x–, que nos incide en la idea anterior de que cada vez hay menos números primos.

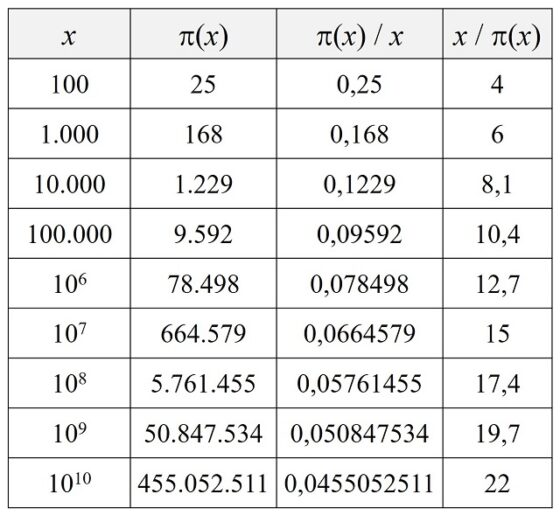
La primera aproximación a la distribución de los números primos vino de la mano del matemático alemán Carl F. Gauss (1777-1855), que, a la edad de 15 años, conjeturó que, aunque no se podía conocer con precisión el valor de la función contador de números primos (x), se podía aproximar con la ayuda de la función logaritmo neperiano. Este resultado, conocido como teorema de los números primos, establece que la función (x) se aproxima a la función x / Ln(x), cuando x tiende a infinito. Este teorema fue demostrado en 1896, de forma independiente, por el matemático francés Jacques Hadamard (1865-1963) y el belga Charles-Jean de la Vallé Poussin (1866-1962). Por ejemplo, si se considera x = 10⁶, como Ln(10⁶) es 6 multiplicado por Ln(10) = 2.30258509…, entonces x / Ln(x) es aproximadamente 72.382, siendo la cantidad de primos 78.498.

El propio Gauss dio una mejor aproximación a la función contador de números primos mediante la función logaritmo integral

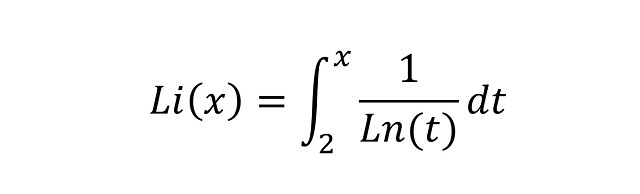
Volviendo al caso de x = 10⁶, mientras que la diferencia de x / Ln(x) con (x) es de 6.116 números, la variación del logaritmo integral Li(x), no os preocupéis ahora de su significado, es sólo de 130.

Pues resulta, que la hipótesis de Riemann, cuya formulación es bastante compleja y está relacionada con los ceros de la conocida función zeta de Riemann que se define sobre los números complejos (ya volveremos sobre ella en alguna futura entrada de Cuaderno de Cultura Científica), es equivalente al hecho de que el logaritmo integral es una “buena” aproximación.

Para terminar

Para cerrar esta entrada del Cuaderno de Cultura Científica, me gustaría incluir los puntos relacionados con las matemáticas del listado de los 97 “consejos para un humano” que escribe el vonadoriano con aspecto de Andrew Martin al final de la historia, que están escritos para “su hijo” (el de Andrew Martin).

Consejo 12: Los telediarios deberían abrir con noticias de matemáticas y seguir con poesía, y a partir de ahí, que hagan lo que quieran.

Consejo 59: Los números son bonitos. Los primos son bonitos. Ya lo entenderás.

Bibliografía

1.- Francois Truffaut, El cine según Hitchcock, Alianza editorial, 1974.

2.- Matt Haig, Los humanos, Roca Editorial, 2014.

3.- R. Ibáñez, La gran familia de los números, Libros de la Catarata, 2021.

Sobre el autor: Raúl Ibáñez es profesor del Departamento de Matemáticas de la UPV/EHU y colaborador de la Cátedra de Cultura Científica

El artículo Los humanos, un Macguffin matemático se ha escrito en Cuaderno de Cultura Científica.