Recursive Walks down User Referral Trees
Recursive Walks Down User Referral TreesMeasuring the total influence of users in a user referral program by traversing indirect referralsWithin many modern software products, there is a chance for users to refer/promote the application to other users. A natural question to ask with these referral programs is: “who is our most influential user promoter of the product?” One naive way to answer this question is to simply count all of the referrals that each user has made, and declare the user with the most referrals to be the most influential.This approach misses critical points. Namely:A user is not rewarded for referring an influential user. I.e. they do not get any credit for referring a user who in turn refers more usersThere is no reward for referring users who pay more. In this approach, a user could refer someone who pays very little, and be deemed just as influential as someone else who referred a high spenderAs a result, we’ll be looking at an alternative way to view this problem. We will instead be taking recursive walks down the referral graphs of users to calculate both the weighted and unweighted total effect of a users referrals.Defining a User Referral TreeA user referral tree is a representation of how users promote a product or service to others, often visualized as a directed graph. In this tree:Nodes represent individual users.Edges represent referral relationships, where a directed edge from user A to user B indicates that user A referred user B.Let’s use the following referral tree as an example:A simple user referral tree (image by author)Here we can see that there are 4 total users in this tree: User A, B, C, and D. We can interpret the arrows as one user referring another user into the product. So, user A has referred two users, User B and User C. In turn, User C has referred one user themself: User D.Toy DataLet’s assume that we are analyzing a SaaS product that sells subscriptions to a television service. There are three tiers of subscription: basic ($10), complete ($20), and pro ($50). The user referral data for this product looks as follows:https://medium.com/media/ab1a0872d428ff92e85e6f28f35f30f8/hrefVisualizing this data, we end up with a directed and disconnected graph structure that looks as such:Example user referral tree (image by author)AnalysisUsing our example data, if we were to use the count of direct referrals as the measure for user influence, we would end up with User D being the most influential (3 direct referrals). However, given what we can see from the graph, we have reason to believe that this may be misleading. Let’s explore some other ways we can approach the problem, using recursive walks down the “referral tree” of every given user.The basic algorithmBasic algorithm for traversing user referrals (image by author)Here, we are simply calculating the number of direct referrals that a user has referred, and recursively adding the number of referrals that each of those direct referrals has given. This rewards users who refer users who in turn refer more users.With this methodology, our most influential user (the one who has the most associated downstream referrals) is User I, whose full referral tree includes 5 users.User A = 2, User D = 4, User I = 5, User F = 1, User J = 1, User K = 2Weighting the algorithmRevenue weighted user referral traversal (image by author)With the previous method, we got a better understanding of the total referral impact of a given user. That method failed to account for the quality of each of these referrals. To proxy referral quality, we are going to be using the amount of revenue that a given user is generating. This amount of revenue will be used as a “weight” on any given referral.As we can see, our most influential user with the method is still User I, when considering the total revenue that a user has directly or indirectly referred.User A = $70, User D = $60, User I = $140, User F = $20, User J = $10, User K = $100Decaying the algorithmDecayed user referral traversal (image by author)Both of the previous methods helped us get a better understanding of the total impact of a user’s referrals. To take this one step further, we might also consider the fact that an indirect referral (i.e. a referral of a referral) is less influenced by that original user. To correct for this fact, we can “decay” or reduce the amount of attribution that a user gets as referral layers get further and further away. There are numerous options for what this decay function could look like, but it will be kept simple here for the purposes of our example. We will simply user a fraction of 1 divided by the current layers of distance.This time, we end up in a tie between User D and User I.User A = 2, User D = 3.5, User I = 3.5, User F = 1, User J = 1, User K = 2Putting it all togetherPutting all of the components together in one traversal formula (image by author)Now all three techniques (recursive counting, revenue weighting, and decayed impact) can be utili
Recursive Walks Down User Referral Trees
Measuring the total influence of users in a user referral program by traversing indirect referrals
Within many modern software products, there is a chance for users to refer/promote the application to other users. A natural question to ask with these referral programs is: “who is our most influential user promoter of the product?” One naive way to answer this question is to simply count all of the referrals that each user has made, and declare the user with the most referrals to be the most influential.
This approach misses critical points. Namely:
- A user is not rewarded for referring an influential user. I.e. they do not get any credit for referring a user who in turn refers more users
- There is no reward for referring users who pay more. In this approach, a user could refer someone who pays very little, and be deemed just as influential as someone else who referred a high spender
As a result, we’ll be looking at an alternative way to view this problem. We will instead be taking recursive walks down the referral graphs of users to calculate both the weighted and unweighted total effect of a users referrals.
Defining a User Referral Tree
A user referral tree is a representation of how users promote a product or service to others, often visualized as a directed graph. In this tree:
- Nodes represent individual users.
- Edges represent referral relationships, where a directed edge from user A to user B indicates that user A referred user B.
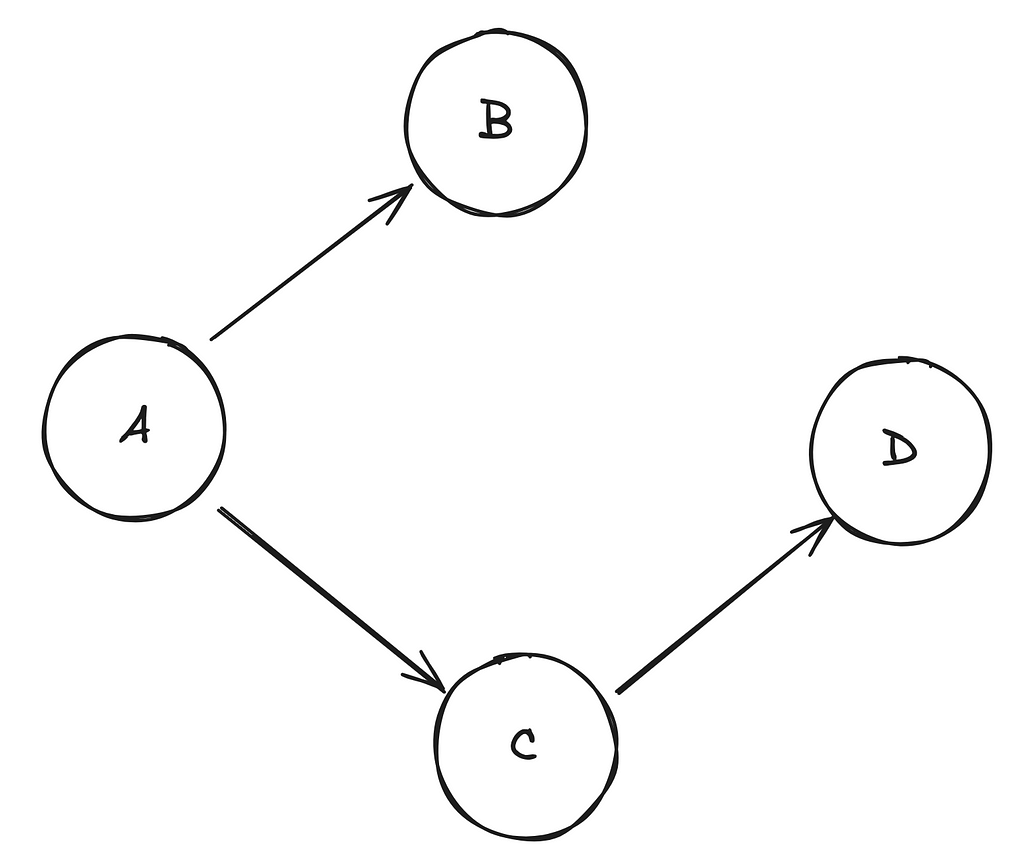
Let’s use the following referral tree as an example:
Here we can see that there are 4 total users in this tree: User A, B, C, and D. We can interpret the arrows as one user referring another user into the product. So, user A has referred two users, User B and User C. In turn, User C has referred one user themself: User D.
Toy Data
Let’s assume that we are analyzing a SaaS product that sells subscriptions to a television service. There are three tiers of subscription: basic ($10), complete ($20), and pro ($50). The user referral data for this product looks as follows:https://medium.com/media/ab1a0872d428ff92e85e6f28f35f30f8/href
Visualizing this data, we end up with a directed and disconnected graph structure that looks as such: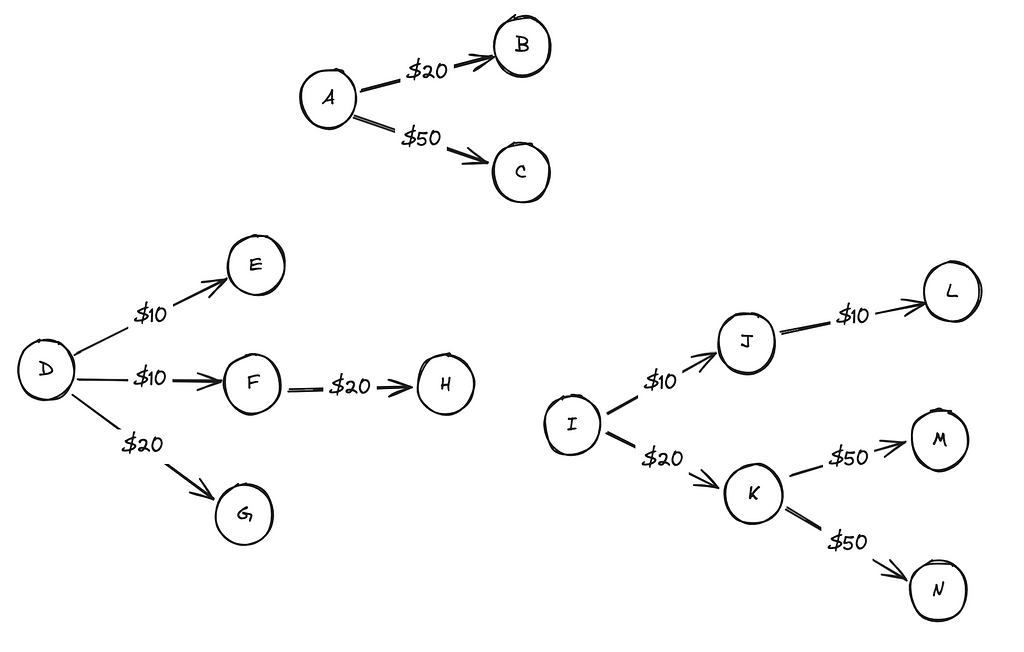
Analysis
Using our example data, if we were to use the count of direct referrals as the measure for user influence, we would end up with User D being the most influential (3 direct referrals). However, given what we can see from the graph, we have reason to believe that this may be misleading. Let’s explore some other ways we can approach the problem, using recursive walks down the “referral tree” of every given user.
The basic algorithm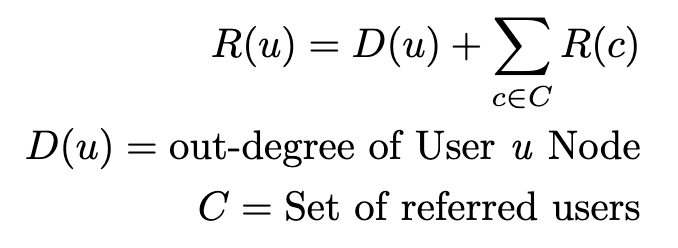
Here, we are simply calculating the number of direct referrals that a user has referred, and recursively adding the number of referrals that each of those direct referrals has given. This rewards users who refer users who in turn refer more users.
With this methodology, our most influential user (the one who has the most associated downstream referrals) is User I, whose full referral tree includes 5 users.
- User A = 2, User D = 4, User I = 5, User F = 1, User J = 1, User K = 2
Weighting the algorithm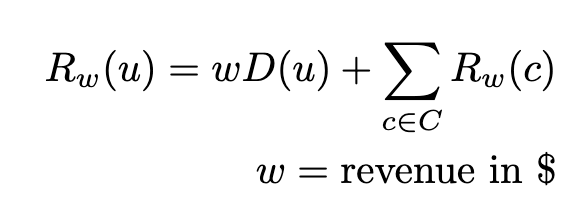
With the previous method, we got a better understanding of the total referral impact of a given user. That method failed to account for the quality of each of these referrals. To proxy referral quality, we are going to be using the amount of revenue that a given user is generating. This amount of revenue will be used as a “weight” on any given referral.
As we can see, our most influential user with the method is still User I, when considering the total revenue that a user has directly or indirectly referred.
- User A = $70, User D = $60, User I = $140, User F = $20, User J = $10, User K = $100
Decaying the algorithm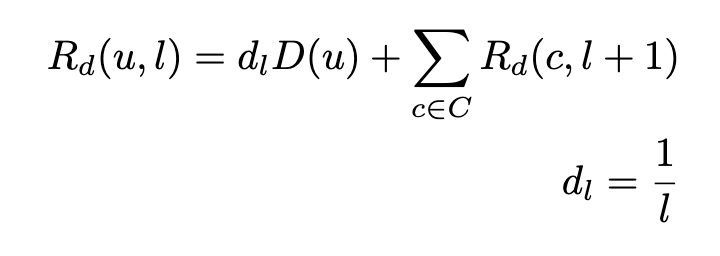
Both of the previous methods helped us get a better understanding of the total impact of a user’s referrals. To take this one step further, we might also consider the fact that an indirect referral (i.e. a referral of a referral) is less influenced by that original user. To correct for this fact, we can “decay” or reduce the amount of attribution that a user gets as referral layers get further and further away. There are numerous options for what this decay function could look like, but it will be kept simple here for the purposes of our example. We will simply user a fraction of 1 divided by the current layers of distance.
This time, we end up in a tie between User D and User I.
- User A = 2, User D = 3.5, User I = 3.5, User F = 1, User J = 1, User K = 2
Putting it all together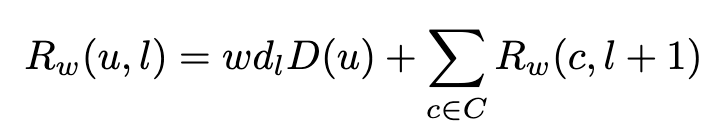
Now all three techniques (recursive counting, revenue weighting, and decayed impact) can be utilized in tandem to get a full picture of which user is having the most impact in our referral tree.
Surprisingly, we now find that User K is our most influential referrer. Although they’ve only referred a couple users, the total direct revenue impact of those users outweighs any other referring user. This decaying of the weighted impact is also why User I has dropped out of being the most influential (much of the weighted impact is happening indirectly)
- User A = $70, User D = $50, User I = $85, User F = $20, User J = $10, User K = $100
Conclusion
Accurately measuring the influence of users in a referral program goes beyond simply counting direct referrals. By leveraging recursive walks down user referral trees, incorporating revenue weights, and applying decay factors, we gain a deeper understanding of specific user impact.
This approach rewards users not just for the quantity but also the quality of their referrals, accounting for both the revenue generated and the cascading influence of their tree. It highlights the importance of a holistic view when assessing referral impact, ensuring that users who contribute to the long-term growth and profitability of the tree are appropriately recognized. Note, the methods presented above are only meant to serve as a starting point, and there are potentially endless ways to adapt the above to arrive at an attribution system that best reflects your product.
Through these methodologies, referral programs can be optimized for influential user patterns, and design incentive structures that align with growth in this area. Ultimately, this refined measurement ensures fair attribution and helps unlock a clearer perspective of referral-driven growth.
Recursive Walks down User Referral Trees was originally published in Towards Data Science on Medium, where people are continuing the conversation by highlighting and responding to this story.
What's Your Reaction?